I love restricted cubic splines, made famous by Frank Harrell (see his approach starting on page 58 here). Dr. Harrell made a package for automating these in R. I’m not aware of an equivalent package for Stata. Here’s my approach to making this specific restricted cubic spline in Stata.

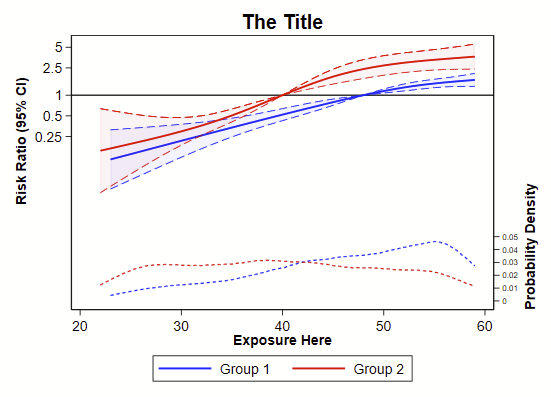
The model here is modified Poisson regression using the Zou 2004 method since the outcome is binary. Since it’s coded as a GLM, it’ll be relatively easy to swap out this one specific model for other models, like logistic regression using the appropriate link & family. It’s good habit to have the probability density of the outcome across the continuum of exposure, so that is plopped on the bottom here. It wouldn’t take much work to replace with a histogram.

This is for two groups (group1=blue, group2=red). It wouldn’t be too hard to make this for just one group, deleting everything having to do with group 2 or having the number 2 in it. Or, duplicate lines for a group 3. Also, sometimes folks like to present a kernel density plot for each outcome, so you’d just duplicate the kdensity lines and add some code to specify that one of each is for folks with outcome==0 then outcome==1.

One quirk is that the xbrcspline code depends on a list of all of the possible options for the exposure, which is brought in from listof to xbrcspline as a numlist. As you can see in –help limits–, numlists are capped at 2,500 numbers. If you get an error saying “values() invalid — invalid numlist has too many elements”, then you have too many individual options for your exposure. This might be because your exposure is an integer with a huge amount of digits after the decimal place, so your >2,500 observations all come with their own unique value for the exposure. Rounding can help reduce this count, if it analytically and clinically makes sense. (This is okay for BMI, for example, because there isn’t clinically relevant difference between a bmi of 27.0400558235 and 27.04). To generate a rounded value, plop —gen bmi_round=(bmi, 0.01)– in the first few lines, right after opening your data. Then use “bmi_round” as your exposure variable rather than “bmi”.

You also should consider centering your exposure variables at the mean. To do this, use the –sum– command for each variable then –gen [variable’s name]_center = [variable’s name]/r(mean)–. Then use the “[variable’s name]_center” as exposures variables.

This code is a mostly rewritten version of one that is used at the Welch Center at Hopkins, where it has been handed down through generations of doctoral students and post-docs.

I’ve recently needed to make these figures using pweights, so I put some comments throughout to simplify that process.

Note: One glitch with WordPress (the blog that hosts this) is that it can’t render certain code below unless it’s the final line in a block of code, so I’ve had to chop it up this script, which should be a single block of code, into several blocks of code. If you copy and paste this into a do file and try to run it, you’ll notice some blank lines in the “Make a Figure” section that you’ll need to delete.

Enjoy!

Code to make the figure above

*************************************************
***************load data!************************
****************and drop any open graphs*********
*************************************************
webuse fvex, clear
graph drop _all
macro drop _all
// if weighted, declare weighting here
*************************************************
**************define variables here**************
*************************************************
// Define the OUTCOME, = to 0 or 1, after the (first) word "outcome"
global outcome outcome // this database's outcome is called outcome...
// Define the EXPOSURE following the word "exposure"
global exposure age // this has to be a continuous variable
// Define the COVARIATES following word "covariate"
global covariates sex distance
// Define what makes GROUP 1 here after "thing1" (blue)
global thing1 if arm==1 
// Define what makes GROUP 2 here after "thing2" (red)
global thing2 if arm==2

*************************************************
************auto-generate subgroups and**********
*****************local macros needed*************
********************for spline*******************
*************************************************
// need to make the exposure by group for the kernel density plots. 
gen exposuresubgroup1 = ${exposure} ${thing1}
gen exposuresubgroup2 = ${exposure} ${thing2}

// The xbrcspine command below needs the middle value of the exposure 
// for each group. This is often times the median, but if there are 
// an even number of values for the exposure, the median will be an 
// average of the two middle values of the exposure variable. The following 
// code defines the median as a local macro (median1temp) then grabs the
// actual value for the exposure closest to that number (median_1). 
// _pctile can be used with pweight, if needed.
//
_pctile exposuresubgroup1, p(50)
// _pctile exposuresubgroup1 [pweight=samplingweight], p(50)
local median1temp = r(r1)
gen mediandiff1=abs(exposuresubgroup1-`median1temp')
gsort mediandiff1
local median_1 = ${exposure}[_n==1]
//
_pctile exposuresubgroup2, p(50)
// _pctile exposuresubgroup2 [pweight=samplingweight], p(50)
local median2temp = r(r1)
gen mediandiff2=abs(exposuresubgroup2-`median2temp')
gsort mediandiff2
local median_2 = ${exposure}[_n==1]
//
// get rid of these variables, since they are not needed anymore
drop mediandiff1 mediandiff2

*************************************************
*************make splines and view knots!********
*************************************************
// NOTE: look at the stata output here, the knots will be displayed
// you'll need to list these in the footer
// 
// Harrell's method recommends using the # of knots ('k') as 3, 4 or 5
// with n >=100 as 5 and n<30 as 3. It's just a guideline. 
// Details are on page 58 here: 
// https://hbiostat.org/doc/rms.pdf
mkspline ${exposure}_spline1=exposuresubgroup1, nknots(4) cubic displayknots
mat knots1=r(knots)
mkspline ${exposure}_spline2=exposuresubgroup2, nknots(4) cubic displayknots
mat knots2=r(knots)
// above won't work for pweight weighted data. instead, you need 
// to specifically define the percentiles from the table on pg 5 here:
// https://www.stata.com/manuals13/rmkspline.pdf
// But basically, 
// 3 knots, percentiles are at: 10 50 90
// 4 knots, percentiles are at: 5 35 65 95
// 5 knots, percentiles are at: 5 27.5 50 72.5 95
// 6 knots, percentiles are at: 5 23 41 59 77 95
// 7 knots, percentiles are at: 2.5 18.33 34.17 50 65.83 81.67 97.5
// the code for 4 knots follows in hidden code:
//
//_pctile exposuresubgroup1 [pweight=samplingweight], p(5 35 65 95) 
//return list
//local gr1knot1 = r(r1)
//local gr1knot2 = r(r2)
//local gr1knot3 = r(r3)
//local gr1knot4 = r(r4)
//di "Knots for group 1 are at " `gr1knot1' ", " `gr1knot2' ", " ///
//`gr1knot3' ", " `gr1knot4' "."
//
//
//mkspline ${exposure}_spline1=exposuresubgroup1,  ///
//knots(`gr1knot1' `gr1knot2' `gr1knot3' `gr1knot4' ) ///
//cubic displayknots
//
//mat knots1=r(knots)
//
//_pctile exposuresubgroup2 [pweight=samplingweight], p(5 35 65 95) 
//return list
//local gr2knot1 = r(r1)
//local gr2knot2 = r(r2)
//local gr2knot3 = r(r3)
//local gr2knot4 = r(r4)
//
//di "Knots for group 2 are at " `gr2knot1' ", " `gr2knot2' ", " ///
// `gr2knot3' ", " `gr2knot4' "."
//
//
//mkspline ${exposure}_spline2=exposuresubgroup2,  ///
//knots(`gr2knot1' `gr2knot2' `gr2knot3' `gr2knot4') ///
//cubic displayknots
//
//mat knots2=r(knots)
*************************************************
********Generate models to use in splines********
*************************************************
// model time!
// the models here are modified poisson regressions using sandwich variance estimators
// which is the Zou method from this classic paper:
// https://pubmed.ncbi.nlm.nih.gov/15033648/
// GLMs can be used with pweight, if needed.
//
// First group 
glm ${outcome} c.${exposure}_spline1* ${covariates}  ${thing1},  ///
fam(poisson) link(log) eform robust
// robust is required for modified poisson regression by zou's method 
// (i.e., modified poisson regression with sandwich variance estimators)
// for pweight or survey data, use:
// svy: glm ${outcome} c.${exposure}_spline1* ${covariates}  ${thing1},  ///
// fam(poisson) link(log) eform
levelsof(${exposure})  ${thing1}  // generates r(levels) for next line
xbrcspline ${exposure}_spline1, values(`r(levels)') ///
ref(`median_1') matknots(knots1) /// 
eform gen(lpnt1 hr1 lb1 ub1)

// Second group
glm ${outcome} c.${exposure}_spline2* ${covariates} ${thing2}, ///
fam(poisson) link(log) eform robust
// for pweight or survey data, use:
// svy: glm ${outcome} c.${exposure}_spline2* ${covariates}  ${thing2},  ///
// fam(poisson) link(log) eform
//
levelsof(${exposure}) ${thing2} // generates r(levels) for next line
xbrcspline ${exposure}_spline2, values(`r(levels)') ///
ref(`median_2') matknots(knots2) /// 
eform gen(lpnt2 hr2 lb2 ub2)

*************************************************
***********generate extremes to drop*************
*************************************************
// should drop the extremes, here the 0.5 and 99.5th percentiles
// but need to define these as local macros.
// _pctile can be used with pweight, if needed.
_pctile exposuresubgroup1, p(0.5 99.5)
return list
local cut_a1 = r(r1)
local cut_b1 = r(r2)

_pctile exposuresubgroup2, p(0.5 99.5)
return list
local cut_a2 = r(r1)
local cut_b2 = r(r2)

*************************************************
***************make the figure*******************
*************************************************
set scheme s1mono // my favorite scheme
twoway ///
/// spline for one group
(line  hr1 lpnt1 if lpnt1 > `cut_a1' & ///
lpnt1 < `cut_b1' , yaxis(1) lp(solid) lc(blue) lwidth(medthick) ) ///

(rarea lb1 ub1 lpnt1 if lpnt1 > `cut_a1' & ///
lpnt1 < `cut_b1' , yaxis(1) color(blue%5)) ///

(line  lb1 lpnt1 if lpnt1 > `cut_a1' & ///
lpnt1 < `cut_b1', yaxis(1)  lp(dash) lc(blue) lwidth(thin) ) ///

(line  ub1 lpnt1 if lpnt1 > `cut_a1' & ///
lpnt1 < `cut_b1' , yaxis(1) lp(dash) lc(blue) lwidth(thin) ) ///

/// spline for other group
(line  hr2 lpnt2 if lpnt2 > `cut_a2' & ///
lpnt2 < `cut_b2' , yaxis(1) lp(solid) lc(red) lwidth(medthick) ) ///

(rarea lb2 ub2 lpnt2 if lpnt2 > `cut_a2' & ///
lpnt2 < `cut_b2' , yaxis(1) color(red%5)) ///

(line  lb2 lpnt2 if lpnt2 > `cut_a2' & ///
lpnt2 < `cut_b2' , yaxis(1)  lp(dash) lc(red) lwidth(thin) ) ///

(line  ub2 lpnt2 if lpnt2 > `cut_a2' & ///
lpnt2 < `cut_b2' , yaxis(1) lp(dash) lc(red) lwidth(thin) ) ///

(line  ub2 lpnt2 if lpnt2 > `cut_a2' & ///
lpnt2 < `cut_b2' , yaxis(1) lp(dash) lc(red) lwidth(thin) ) ///

/// kernel density for one group
/// note: can alternatively install kdens and moremata to 
/// use pweighting in kernel density.
(kdensity exposuresubgroup1 if exposuresubgroup1 > `cut_a1' & ///
exposuresubgroup1 < `cut_b1' , yaxis(2) lp(shortdash) lcolor(blue)) ///

/// kernel density for other group
(kdensity exposuresubgroup2 if exposuresubgroup2 > `cut_a2' & ///
exposuresubgroup2 < `cut_b2' , yaxis(2) lp(shortdash) lcolor(red)) ///

, ///
yline(1, lpattern(solid) lcolor(black) axis(1)) ///
/// labels for the left axis, hide the following line if you aren't sure 
/// of what the range should be:
ylabel(0.25 "0.25" 0.5 "0.5" 1 "1" 2.5 "2.5" 5 "5", axis(1) angle(0)) ///
/// range for the left axis. the BOTTOM of this range has to be WAAAY lower 
/// than the bottom ylabel in the line above in order for it to sit 
/// on the way top of the figure. 
yscale(r(0.001 2) log axis(1)) /// log scale here
/// ditto for the right axis, but the TOP of the range on the yscale needs 
/// to be WAAAY higher than the top ylabel
ylabel(0 "0" 0.01 "0.01" 0.02 "0.02" 0.03 "0.03" 0.04 "0.04" 0.05 "0.05", ///
axis(2) labsize(vsmall) angle(0)) ///
yscale(r(0.0 .2) axis(2)) /// not log scale here
/// you'll notice that the x label doesn't span the entire 
/// range of the exposure because the local macro cuts above. 
///xlabel(20(5)60) in case you want to specify the x axis
/// for the titles, need to put a bunch of spaces so things align
ytitle("                {bf:Risk Ratio (95% CI)}", axis(1)) ///
ytitle("{bf:Probability Density}                                          ", ///
 justification(left) axis(2)) ///
xtitle("{bf:Exposure Here}") ///
title("{bf:The Title}") ///
legend(order(1 "Group 1" 5 "Group 2")) ///
name(mygraph1)
			
*************************************************
*****************Save figure!********************
*************************************************
// save as png, change to tif if needed for submission			
graph export "mygraph1.png", replace width(1000)