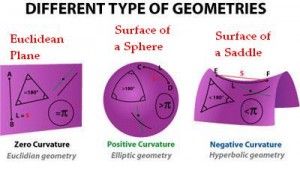
Euclidian geometry has its origins in Alexander’s Greece. It is a logical system of geometry, based on Euclid’s Elements, which predominated the world of geometry for around 2000 years. In Euclidian geometry, in which all theorems originate from Euclid’s postulates, most notably the parallel postulate, which states that on a plane, at a given point not on a line, at most one other line can be drawn which does not intersect that line. Other notable postulates include: the theory of straight lines being two points connected infinitely, a circle being a certain distance(radius) from one point, that all right angles are equal, etc… This was the only accepted system until the 19th century.
In the 19th century, scientists like Carl Friedrich Gauss, Ferdinand Karl Schweikart, Janos Bolyai, and Nikolai Lobachevsky pioneered the field of non-Euclidian, or hyperbolic geometry, though none of them worked together to do so. In this geometry, many of Euclid’s postulates are satisfied, but not the parallel postulate. For example, the sum of the angles of a triangle is less than 180 degrees, and triangles with the same angles have the same area. Conversely, in Elliptical geometry, the sum of the angles of a triangle is greater than 180 degrees
Depiction of Three Forms of Geometry
Source: www.blendspace.com
Non-Euclidian geometry opened up the possibility of a fourth dimension, which was being widely talked about at the time of Flatland’s publishing. It took the lid off of Pandora’s box for geometry. Abbott was no doubt inspired by these new theories, and they allowed him to create the fictional worlds of Spaceland, Flatland, Lineland, and Pointland.
Sources:
Wolfe, Harold Eichholtz. Introduction to Non-Euclidean Geometry. New York: Dryden, 1945. Print.